Comparing datasets with LMM¶
It is not straightforward to define a p-Value for RT-DC data (e.g. change in deformation for a treatment vs. its control). This is somewhat counter-intuitive, because one could assume that the large number of events in a single dataset should be enough to compare two datasets. Focus changes, chip-to-chip variations, etc. may generate systematic offsets which make a direct comparison (e.g. t-Test) impossible. Linear mixed models (LMM) allow to assign a significance to a treatment (fixed effect) while considering the systematic bias in-between the measurement repetitions (random effect).
Shape-Out offers a LMM analysis as described in [Herbig2018]. The LMM analysis is performed using the lme4 R package. Here, we make use of the dataset [FigshareLMM] to illustrate this functionality.
Basic linear mixed models¶
We would like to quantify the difference between human skeletal stem cells (SSC) and the human osteosarcoma cell line MG-63 (which is often used as a model system for SSCs) using a likelihood ratio test based on LMM.
From the dataset [FigshareLMM], load the following files into Shape-Out:
- SSC_16uls_rep1_20150611.rtdc (SSC repetition 1)
- SSC_16uls_rep2_20150611.rtdc (SSC repetition 2)
- MG63_pure_16uls_rep1_20150421.rtdc (MG-63 repetition 1)
- MG63_pure_16uls_rep2_20150422.rtdc (MG-63 repetition 2)
- MG63_pure_16uls_rep3_20150422.rtdc (MG-63 repetition 3)
In this example, we treat SSC as our “treatment” and MG-63 as our “control”. These are just names that remind us that we are comparing one type of sample against another type.
In the Filter tab, please choose the following Box filters:
- Porosity (area_ratio): 0 to 1.05
- Area [µm²] (area_um): 120 to 550
- Deformation (deform): 0 to 0.1
Hit Apply and proceed to the Calculate tab. We would also like to have a look at the Young’s modulus. The medium (CellCarrier) and the temperature (23°C) should already be set. Hit Compute elastic modulus to make the Young’s modulus available.
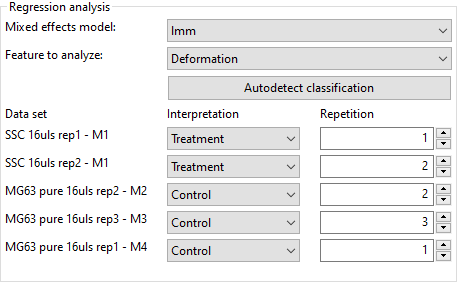
Proceed to the Analyze tab. Set the Interpretation and Repetition according to the following scheme (see screenshot):
- SSC: Treatment
- MG63: Control
- Repetition according to the file/sample name
Make sure that the feature “Deformation” is selected and hit Apply. The results of the LMM analysis are shown in your default text editor:
LINEAR MIXED MODEL:
Linear mixed model fit by REML ['lmerMod']
Formula: xs ~ treatment + (1 + treatment | timeunit)
Data: RTDC
REML criterion at convergence: -34724.9
Scaled residuals:
Min 1Q Median 3Q Max
-2.0760 -0.7148 -0.1546 0.5299 5.3384
Random effects:
Groups Name Variance Std.Dev. Corr
timeunit (Intercept) 0.000e+00 0.000e+00
treatmentTreatment 5.438e-23 7.374e-12 NaN
Residual 1.592e-04 1.262e-02
Number of obs: 5883, groups: timeunit, 3
Fixed effects:
Estimate Std. Error t value
(Intercept) 0.0319279 0.0002052 155.58
treatmentTreatment -0.0013548 0.0003433 -3.95
Correlation of Fixed Effects:
(Intr)
trtmntTrtmn -0.598
COEFFICIENT TABLE:
(Intercept) treatmentTreatment
1 0.03192788 -0.001354766
2 0.03192788 -0.001354766
3 0.03192788 -0.001354766
LIKELIHOOD RATIO TEST (MODEL VS. NULLMODEL):
Data: RTDC
Models:
NullModel: xs ~ (1 + treatment | timeunit)
Model: xs ~ treatment + (1 + treatment | timeunit)
Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
NullModel 5 -34738 -34705 17374 -34748
Model 6 -34743 -34703 17377 -34755 6.2303 1 0.01256 *
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The most important numbers are:
- Fixed effects (Intercept)-Estimate: The mean of the parameter chosen for all controls.
- Fixed effects treatment-Estimate: The effect size of the parameter chosen between the mean of all controls and the mean of all treatments.
- Full coefficient table: Shows the effect size of the parameter chosen between control and treatment for every single experiment.
- Model-Pr(>Chisq): Shows the p-value and the significance of the test.
We are interested in the p-value, which is 0.01256 for Deformation. We repeat the analysis with Area (0.0002183) and Young’s modulus (0.0002771). The p-values indicate that MG-63 (mean elastic modulus 1.26 kPa) cells are softer than SSCs (mean elastic modulus 1.54 kPa) [Herbig2018].
Important
Why are the p-values different when I swap repetitions in LMM analysis?
(A comment by Maik Herbig)
If this happens, you essentially changed the pairing of measurements. In Shape-Out you can determine the “Repetition number” of your experiment. If the same repetition number is chosen for a “Control” and a “Treatment” measurement, a paired test will be conducted. In your experimental design you determine which measurements are paired, before doing any experiments. Do not start to pair experiments after you have seen the data to obtain the lowest p-value (this would be p-hacking). For example you could decide to measure one “control” and one “treated” sample on three consecutive days. Then, it makes sense to pair the measurements of the same day. Oftentimes this is not possible and you have to measure 3x “control” on one day and 3x “treated” on the next day. Then you could for example pair the first measurement of “control” with the first measurement of “treated” and the second of “control” with the second of “treated” and so on.
Alternatively, you can also run an an unpaired test by just giving each measurement a different “Repetition” number. For example when having 3x “control” and 3x “treatment” you could give it numbers from 1 to 6.
LMM analysis of differential deformation¶
The LMM analysis is only applicable if the feature chosen is not pronounced visibly in the reservoir measurements. For instance, if a treatment results in non-spherical cells in the reservoir, then the deformation recorded for the treatment might be biased towards higher values. In this case, the information of the reservoir measurement has to be included by means of differential deformation [Herbig2018]. The idea of differential deformation is to subtract the reservoir from the channel deformation. Since it is not possible to assign the events in the reservoir to the events in the channel (two different measurements), bootstrapping is employed which generates statistical representations of the two measurements that can then be subtracted from one another. Then, for the actual LMM analysis, only the differential deformation is used.
For differential deformation analysis, we need for each repetition a reservoir measurement (e.g. Treatment 1 and Reservoir Treatment 1). From the dataset [FigshareLMM], load the following files into Shape-Out and proceed with filtering as described above:
- SSC_16uls_rep1_20150611.rtdc (SSC repetition 1)
- SSC_16uls_rep2_20150611.rtdc (SSC repetition 2)
- SSC_reservoir_rep1_20150611.rtdc (SSC reservoir repetition 1)
- SSC_reservoir_rep2_20150611.rtdc (SSC reservoir repetition 2)
- MG63_pure_16uls_rep1_20150421.rtdc (MG-63 repetition 1)
- MG63_pure_16uls_rep2_20150422.rtdc (MG-63 repetition 2)
- MG63_pure_16uls_rep3_20150422.rtdc (MG-63 repetition 3)
- MG63_pure_reservoir_rep1_20150421.rtdc (MG-63 reservoir repetition 1)
- MG63_pure_reservoir_rep2_20150422.rtdc (MG-63 reservoir repetition 2)
- MG63_pure_reservoir_rep3_20150422.rtdc (MG-63 reservoir repetition 3)

In the Analyze tab, there are now ten measurements to assign. Proceed as above, using the sample names as indicator for treatment/control and repetition (see screenshot).
Note
The data sets are ordered according to run index. In an ideal case, the run index would resemble the repetition of an experiment. Here, however, the run index is only an internal lab book reference.
The results read as follows:
LINEAR MIXED MODEL ON BOOTSTAP-DISTRIBUTIONS:
Linear mixed model fit by REML ['lmerMod']
Formula: xs ~ treatment + (1 + treatment | timeunit)
Data: RTDC
REML criterion at convergence: -59591.1
Scaled residuals:
Min 1Q Median 3Q Max
-6.5206 -0.5391 0.0077 0.5700 6.3890
Random effects:
Groups Name Variance Std.Dev. Corr
timeunit (Intercept) 2.939e-07 0.0005421
treatmentTreatment 1.273e-06 0.0011284 -1.00
Residual 3.862e-07 0.0006215
Number of obs: 5000, groups: timeunit, 3
Fixed effects:
Estimate Std. Error t value
(Intercept) 0.0205095 0.0003132 65.49
treatmentTreatment -0.0052991 0.0006518 -8.13
Correlation of Fixed Effects:
(Intr)
trtmntTrtmn -1.000
COEFFICIENT TABLE:
(Intercept) treatmentTreatment
1 0.01993562 -0.004104567
2 0.02058056 -0.005447047
3 0.02101226 -0.006345642
LIKELIHOOD RATIO TEST (MODEL VS. NULLMODEL):
Data: RTDC
Models:
NullModel: xs ~ (1 + treatment | timeunit)
Model: xs ~ treatment + (1 + treatment | timeunit)
Df AIC BIC logLik deviance Chisq Chi Df Pr(>Chisq)
NullModel 5 -59605 -59572 29807 -59615
Model 6 -59613 -59574 29813 -59625 10.584 1 0.001141 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
The p-value for the differential deformation is 0.001141 which is a magnitude lower than the p-value for the (non-differential) deformation above. This indicates that there is a non-negligible initial deformation of the cells in the reservoir.
Attention
Differential LMM analysis does not make sense for all features. For instance, differential area will yield high values, because the measured area in the reservoir and the sample are similar. Thus, the LMM analysis is performed with distributions that are all centered around zero, yielding no significant difference.
Generalized linear mixed models (GLMM)¶
Shape-Out also makes available one GLLM.
The implementation uses the function glmer (instead of lmer for LMM)
from the lme4 R package. It employs an additional log-link function using
the family keyword argument (family=Gamma(link='log')). The Gamma
function is used generally for data that are continuous and non-negative.
The log-link function is useful if the feature distribution is log-normal.
The log-link function exponentiates the linear predictors of the LMM
(It does not log-transform the outcome variable).
Log-normal behaviour is a quite common, especially in biology. When a physical parameter has a lower limit, and the measured values are close to that limit, the resulting distribution will be skewed, resembling a log-normal distribution. In case of RT-DC this is specially (but not only) true for deformation. Another example is area, which also has a lower limit of zero and may therefore have a skewed distribution. While GLMMs are designed to handle skewed data, it was shown that LMMs already deliver robust results, even for highly skewed data [gelman_hill_2006].
Warning
As we learned above, the decision whether to use LMM or GLMM is not particularly important. Ideally, both LMM and GLMM are consistent. However, never perform both analyses only to then pick the one with the lowest p-value. This is p-hacking! The analysis routine should be defined beforehand. If in doubt, stick to LMM.