Young’s Modulus¶
With Shape-Out, it is possible to convert deformation values to values of the Young’s modulus based on numerical simulation for fully elastic spheres according to Mokbel et al. [MMM+17].
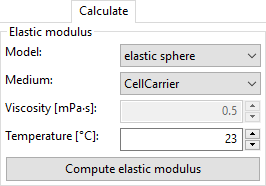
The “Calculate” tab allows you to obtain the Young’s modulus for the samples in the current analysis. After choosing the type of measurement medium you must set the right temperature or – in case you choose “Other” – the correct viscosity. For CellCarrier media, the correct viscosity is automatically calculated, taking shear-thinning into account as discussed in [Her17].
Once “Compute elastic modulus” is clicked, the Young’s modulus will become available for plotting and data analysis.
Validity:
The computation of the Young’s modulus is valid only for objects that initially have a spherical shape. In addition, the deformation and size values must be in a “valid region”. Events outside this region will have a nan-valued (not a number) Young’s modulus. Note that as a result, these events will be excluded from all plots when remove invalid events is checked in the Filter configuration tab.
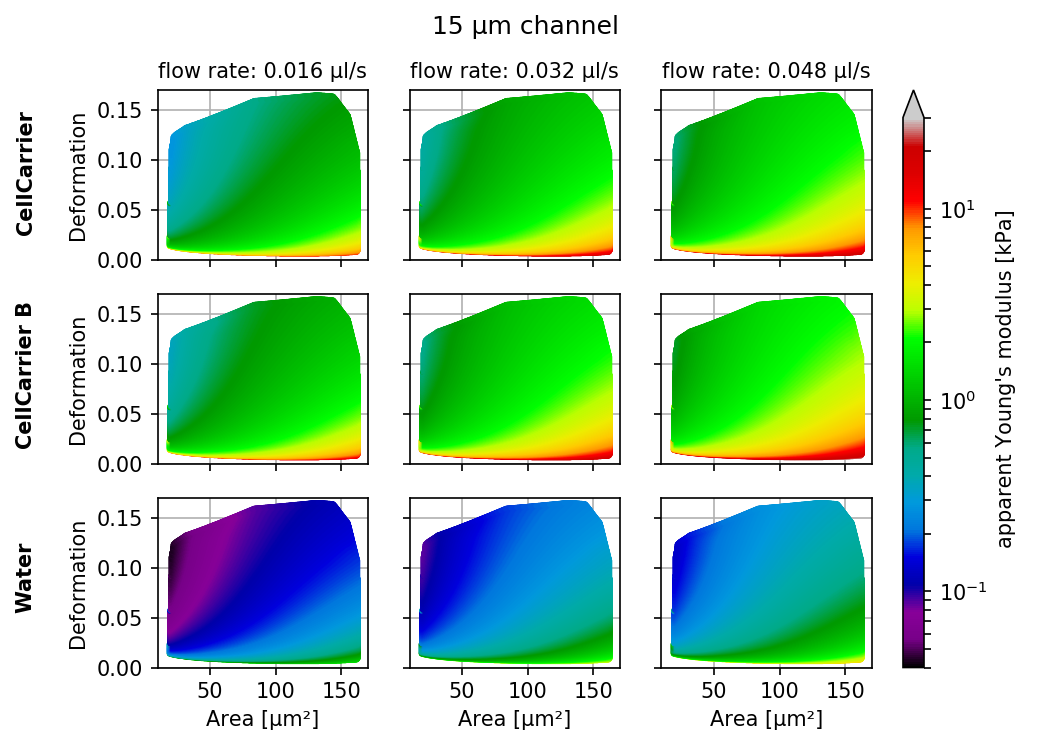
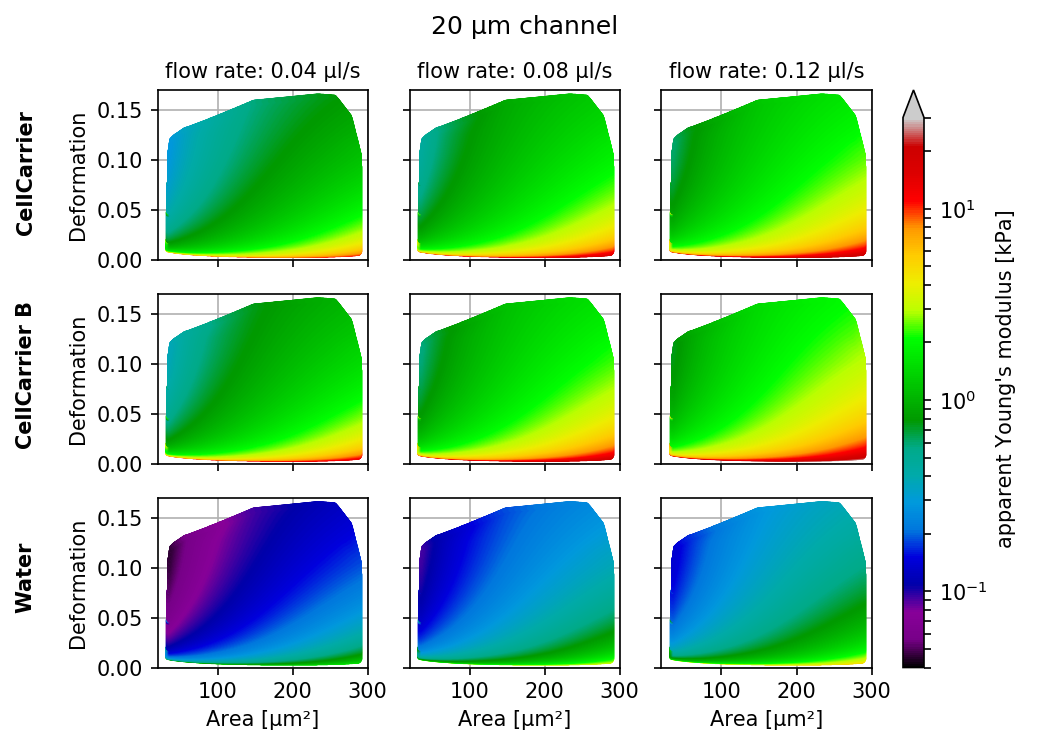
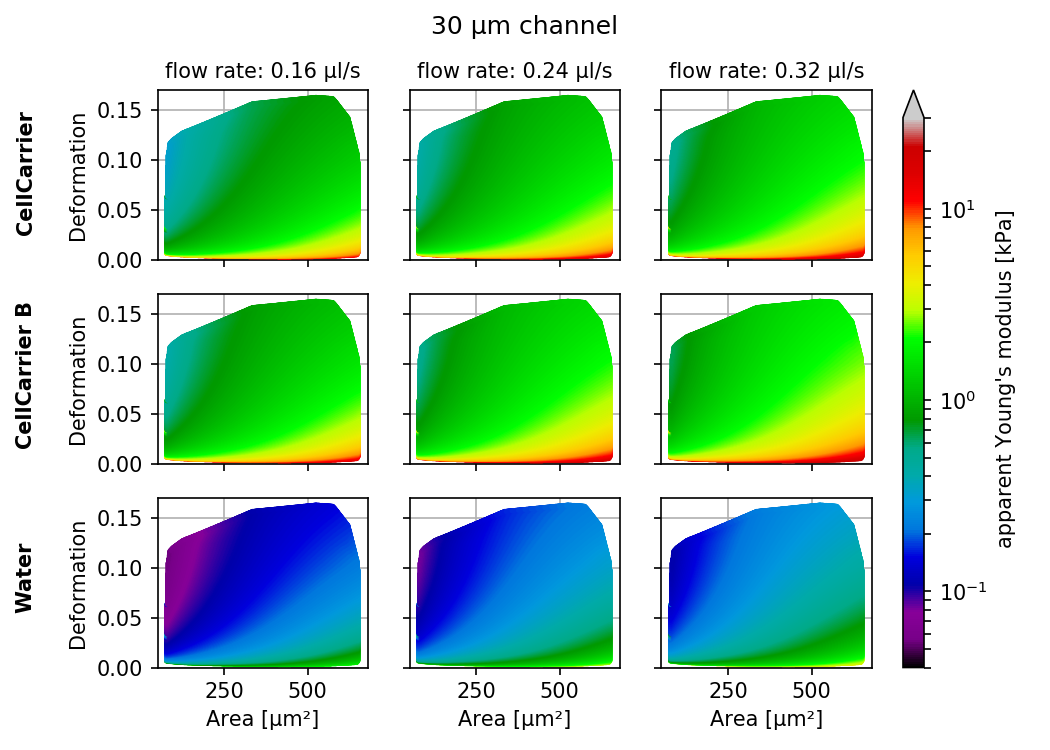
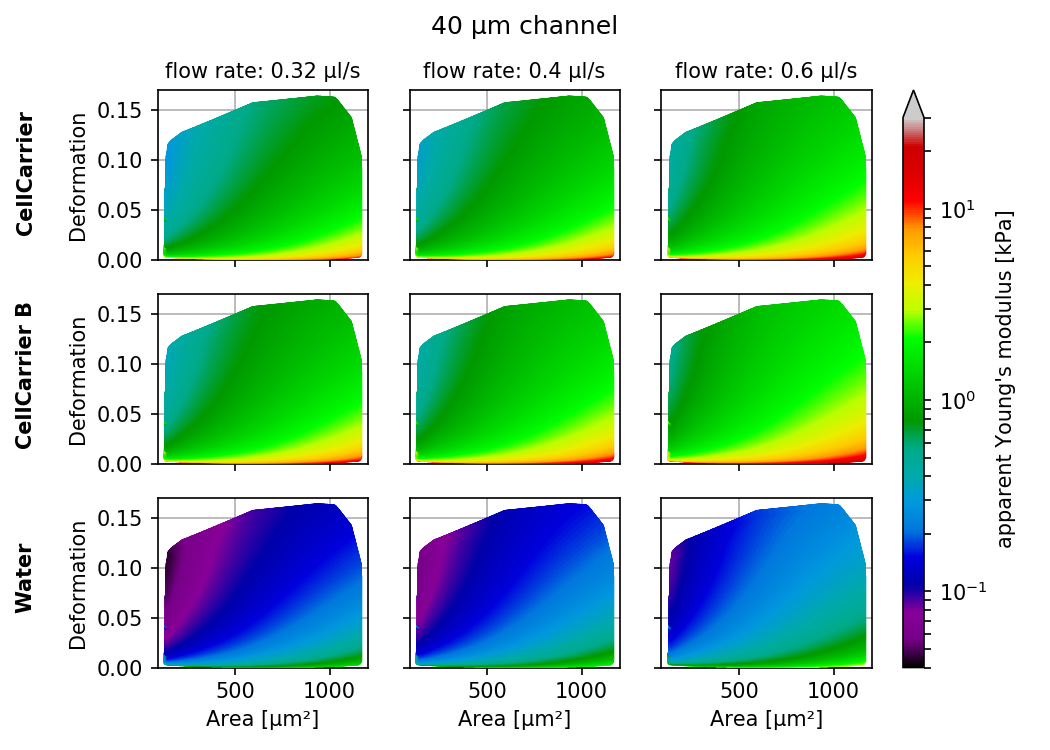
Visualizations of the support and the values of the look-up table (LUT) used for determining the Young’s modulus from deformation and cell area. The values of the Young’s moduli in the regions shown depend on the channel size, the flow rate, the temperature, and the viscosity of the medium [MOG+15]. Here, they are computed for a 15 µm wide channel at 24°C with an effective pixel size of 0.34 µm. The data are corrected for pixelation effects according to [Her17].
The invalid regions (white in the figure above) include objects that are very small or objects with very low deformation values. The reason for that is a very steep increase of the Young’s modulus with little decrease in deformation that could potentially result in very large simulation errors. In addition, regions with high deformation are invalid as well, because the simulations do not converge (objects simulated with lower Young’s moduli become more and more elongated until they rupture). In practice, this means that the channel size has to be selected carefully to match the object sizes. Larger object sizes require wider channels if meaningful values for the Young’s modulus are to be computed.
In the following, additional visualizations for commonly used channel sizes and flow rates are shown: